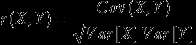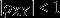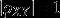曲谱自学网今天精心准备的是《spss相关性分析》，下面是详解！

怎样用spss分析这两组数据的相关性

朋友，你这个数据可采用pearson相关分析就可以，spss的步骤如下：
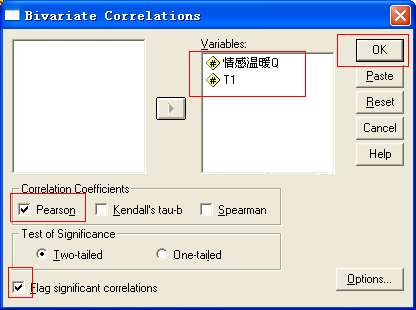
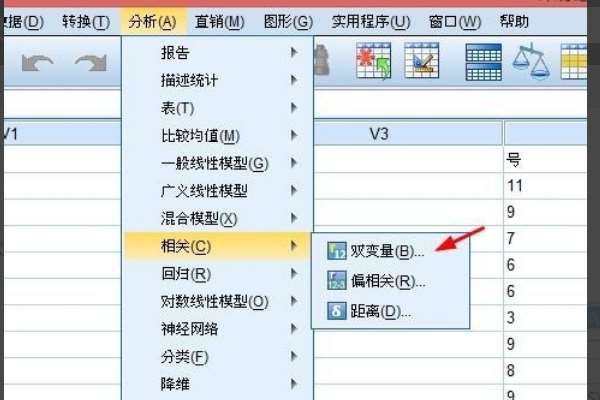
1、单击Analyze——Correlate——Bivariate...，则弹出相关分析Bivariate Correlations对话框
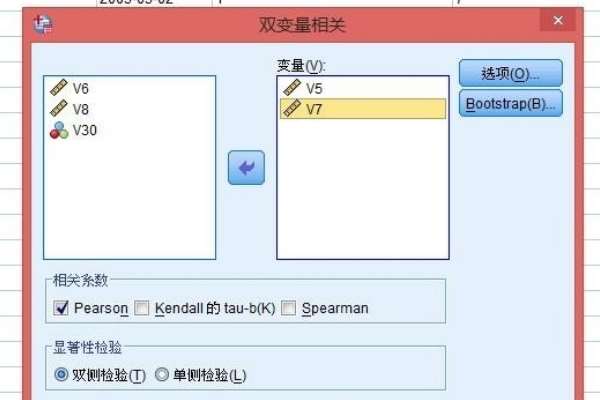
2、把左边的源变量（情感温暖Q和T1）调入右边的矩形框内，同时勾选Pearson选项（见下图）

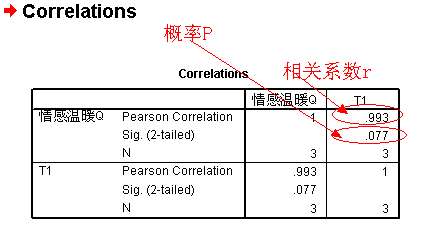
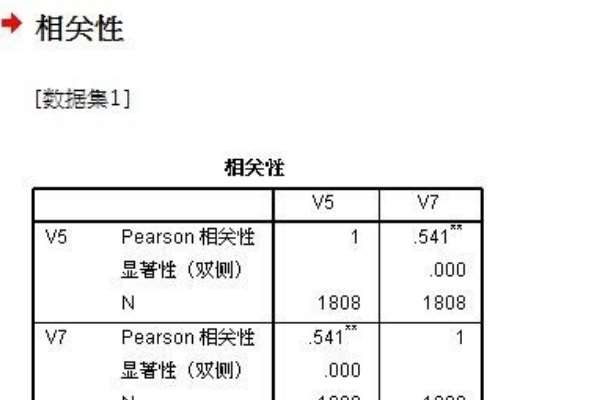
3、点击OK即可，出现如下结果

扩展

这分析出来，有没有意义？是怎样看的？

补充

比如，上面那个概率P值=0.077＞0.05，就可以认为情感温暖与T1之间不存在显著相关性，请吧

spss相关性分析 相关性

相关性X1X2X3X4X5X6X7X8X1Pearson相关性1-.022-.447.999**.999**.982**.994**.975**显著性（双侧）.972.451.000.000.003.001.005N55555555X2Pearson相关性-.0221.261-.059-.025-.179-...

相关性
X1 X2 X3 X4 X5 X6 X7 X8
X1 Pearson 相关性 1 -.022 -.447 .999** .999** .982** .994** .975**
显著性（双侧） .972 .451 .000 .000 .003 .001 .005
N 5 5 5 5 5 5 5 5
X2 Pearson 相关性 -.022 1 .261 -.059 -.025 -.179 -.117 -.206
显著性（双侧） .972 .671 .925 .969 .773 .852 .740
N 5 5 5 5 5 5 5 5
X3 Pearson 相关性 -.447 .261 1 -.481 -.415 -.405 -.448 -.469
显著性（双侧） .451 .671 .413 .488 .499 .450 .426
N 5 5 5 5 5 5 5 5
X4 Pearson 相关性 .999** -.059 -.481 1 .997** .982** .994** .977**
显著性（双侧） .000 .925 .413 .000 .003 .001 .004
N 5 5 5 5 5 5 5 5
X5 Pearson 相关性 .999** -.025 -.415 .997** 1 .985** .994** .975**
显著性（双侧） .000 .969 .488 .000 .002 .001 .005
N 5 5 5 5 5 5 5 5
X6 Pearson 相关性 .982** -.179 -.405 .982** .985** 1 .996** .995**
显著性（双侧） .003 .773 .499 .003 .002 .000 .000
N 5 5 5 5 5 5 5 5
X7 Pearson 相关性 .994** -.117 -.448 .994** .994** .996** 1 .994**
显著性（双侧） .001 .852 .450 .001 .001 .000 .001
N 5 5 5 5 5 5 5 5
X8 Pearson 相关性 .975** -.206 -.469 .977** .975** .995** .994** 1
显著性（双侧） .005 .740 .426 .004 .005 .000 .001
N 5 5 5 5 5 5 5 5
**. 在 .01 水平（双侧）上显著相关。
求结果分析 展开

一般直接看相关系数和显著性双侧。你这个一列一列的看要方便些，比如第一列，表示为x1和其他各变量之间的相关性，x1和x2的相关系数为-.022，显著性双侧为0.972，说明这两个变量间无相关性，依次类推。只要是显著性<0.05即可说明两变量具有相关性，而相关性的大小取决于相关系数，相关系数越接近1，相关性越好。看了一下你的x1和x4-x8的相关系数都在0.9以上了。是非常好的。

怎样用spss分析这两组数据的相关性？

用spss分析两组数据的相关性步骤如下：

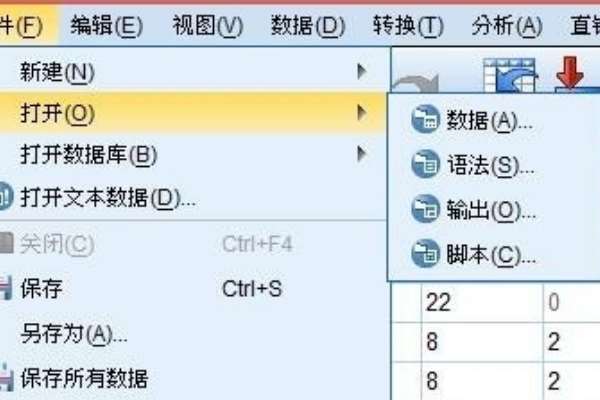
1、第一步，电脑安装SPSS软件包，最好使用最新版本，功能比较齐全。打开SPSS软件，导入你需要分析的数据，这里以excel数据为例子。依次点击【文件】-【打开】-【数据】。

2、第二步，选择excel数据，确认导入后，查看数据是否导入正常。

3、第三步，进行相关性分析。依次点击【分析】-【相关】-【双变量】。

4、第四步，然后，把变量从左侧选择到右侧变量框里面，勾选person相关，双侧检验等等。

5、第五步，点确定，相关性的结果就在输出文档里面了。你也可以把结果复制导出到word或者excel。

这样就完成了用spss分析两组数据的相关性。

如何用spss做相关性分析？？要求详细步骤！

偏相关

从菜单中选择：

分析

相关

偏相关...

选择两个或更多要为之计算偏相关的数值变量。

E 选择一个或多个数值控制变量。

还可以使用以下选项：

􀂄 显著性检验。您可以选择双尾概率或单尾概率。如果预先已知关联的方向，请选

择单尾。否则，请选择双尾。

􀂄 显示实际显著性水平。缺省情况下，将显示每个相关系数的概率和自由度。如果

取消选择此项，则使用单个星号标识显著性水平为0.05 的系数，使用两个星号

标识显著性水平为0.01 的系数，而不显示自由度。此设置同时影响偏相关矩阵

和零阶相关矩阵。

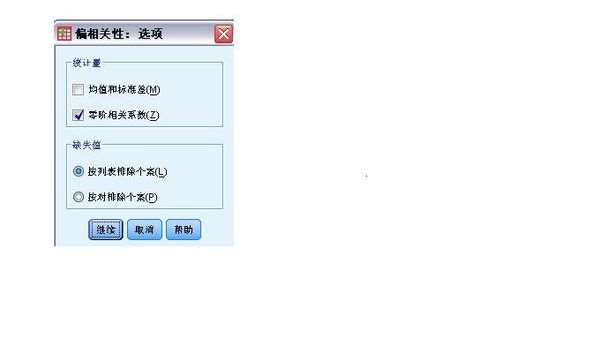
偏相关：选项

“偏相关性: 选项”对话框

统计量。可以选择以下方式中的一个或两个都选：

􀂄 均值和标准差。为每个变量显示。还显示具有非缺失值的个案数。

􀂄 零阶相关系数。显示所有变量（包括控制变量）之间简单相关的矩阵。

缺失值。您可以选择以下选项之一：

􀂄 按列表排除个案。将从所有计算中排除其任何变量（包括控制变量）具有缺失值

的个案。

􀂄 按对排除个案。对于偏相关所基于的零阶相关的计算，不使用其一对变量或其中一个

变量具有缺失值的个案。按对删除可以充分使用数据。但是，个案数可能随系数的

不同而不同。如果按对删除有效，则某个特定的偏相关系数的自由度是基于在任何

零阶相关计算中使用的最小个案数。

请问spss相关分析结果怎么看？

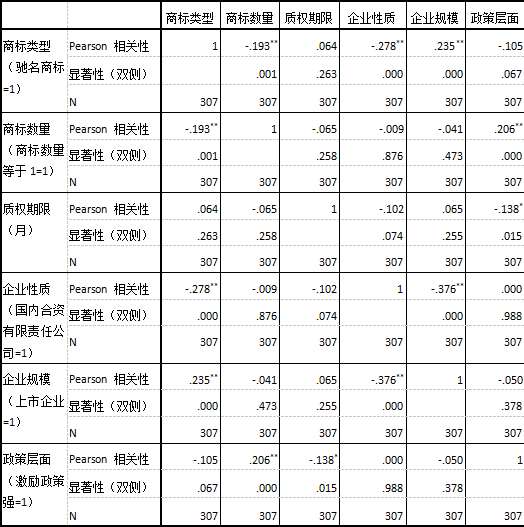
spss 的相关表格每个单元格有三行数据，一个是pearson相关系数值，它代表了相关系数的大小，一个是样本容量，代表你这组数据有多少被试，最后一个是显著性检验结果，即sig（双侧），它可以用来说明你所得到的相关分析结果有没有统计学意义，通常sig<0.05即认为显著，有统计学意义（有统计学意义或者说显著的意思是说这种相关性可以分辨出来，不表示相关的大小，就好像用显微镜可以看到细胞并不能说明细胞很大），如果不显著，即便相关系数很大，也不能说明该相关有意义，相关性有可能是抽样误差所致，但这个时候你可以考虑增大样本容量后再分析看看。相关系数值后面的星号也反映了显著性，一个*表明0.05水平显著，**代表0.01水平显著

更多扩展补充

扩展

哦，也就是说我的图片里面没有几个是有统计学意义的了，对么？

补充

有一个是显著的，其他的都不显著，而且相关系数小，说明效应值本来就不大。可能实际意义确实不大

扩展

大神，那这张图呢？

补充

刚才判断的依据已经说过了，你看里面有星号的就是显著的，即有统计学意义的，其他的就是不显著的。

spss中相关分析中显著相关显著怎么理解

显著相关的“显著”表达的是一个概率。spss对相关性原理是这样的：在假设变量之间的相关性为零的原假设下，根据已有数据算出“相关性=0”的概率，即所谓的P值是多少，之后与设定的显著性水平（通常是5%）相比，如果P<5%，则说明原假设“相关性=0”出现的概率极其微小，几乎不可能存在，换言之，有超过95%的概率说明变量之间存在相关性，也就是显著相关。反之，当P>5%，则“相关性=0”（不相关）会在一定概率下发生，不能完全否定不相关的发生，此时，变量的相关性就不显著了。

spss相关性分析结果看不懂，帮忙解释下~谢了

我做的是学习成绩和学习策略相关性分析。这是一类成绩学生的分析。怎么才能看出那些呈显著相关？麻烦了点击图片可见大图R统计量的值在哪里？那是什么？负相关代表什么？...

我做的是学习成绩和学习策略相关性分析。这是一类成绩学生的分析。怎么才能看出那些呈显著相关？麻烦了
点击图片可见大图
R统计量的值在哪里？那是什么？
负相关代表什么？

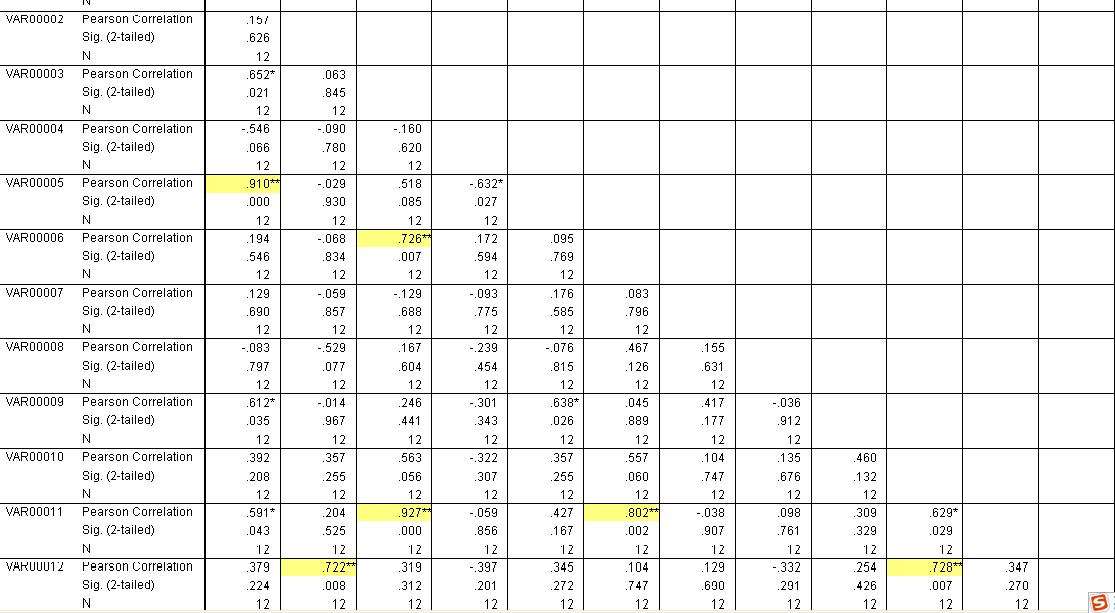
在这个图表中，你说的R值就是皮尔逊相关系数~（pearson correlation）

r>0 代表两变量正相关，r<0代表两变量负相关。

|r|大于等于0.8时，可以认为两变量间高度相关；
|r|大于等于0.5小于0.8时，可以认为两变量中度相关；
|r|大于等于0.3小于0.5时，可以认为两变量低度相关。
小于0.3说明相关程度弱，基本不相关。

上面说了啊~表格里的pearson correlation，就是R值
表格里黄色加重的几个r值，是呈现显著相关的。
简单来说，
正相关是一个变量变大，另一个变量也变大
负相关就是一个变量变大，另一个变量变小

用SPSS进行的相关性分析，不太懂，麻烦给详细说明...

首先你要知道怎么选择这两个方法
如果都满足正态性就选择第二个pearson相关系数，否则第一个
其次看sig小于0.05说明相关系数有统计学意义，小于0.4弱相关
0.4-0.7中等相关，大于0.7强相关。所以你数学成绩和思维是存在中等正相关

spss相关性分析

想用spss分析“自身学习素质”与“学习能力”的相关性，但自身学习素质下面包含5个选项，改如何分析呢？是要把这5个选项合并成一个“自身学习素质”的得分，然后在分析与学习能力的相...

想用spss分析“自身学习素质”与“学习能力”的相关性，但自身学习素质下面包含5个选项，改如何分析呢？是要把这5个选项合并成一个“自身学习素质”的得分，然后在分析与学习能力的相关性吗？ 求指教..谢谢 展开

偏相关
从菜单中选择：
分析
相关
偏相关...
选择两个或更多要为之计算偏相关的数值变量。
E 选择一个或多个数值控制变量。
还可以使用以下选项：
􀂄 显著性检验。您可以选择双尾概率或单尾概率。如果预先已知关联的方向，请选
择单尾。否则，请选择双尾。
􀂄 显示实际显著性水平。缺省情况下，将显示每个相关系数的概率和自由度。如果
取消选择此项，则使用单个星号标识显著性水平为0.05 的系数，使用两个星号
标识显著性水平为0.01 的系数，而不显示自由度。此设置同时影响偏相关矩阵
和零阶相关矩阵。
偏相关：选项
“偏相关性: 选项”对话框
统计量。可以选择以下方式中的一个或两个都选：
􀂄 均值和标准差。为每个变量显示。还显示具有非缺失值的个案数。
􀂄 零阶相关系数。显示所有变量（包括控制变量）之间简单相关的矩阵。
缺失值。您可以选择以下选项之一：
􀂄 按列表排除个案。将从所有计算中排除其任何变量（包括控制变量）具有缺失值
的个案。
􀂄 按对排除个案。对于偏相关所基于的零阶相关的计算，不使用其一对变量或其中一个
变量具有缺失值的个案。按对删除可以充分使用数据。但是，个案数可能随系数的
不同而不同。如果按对删除有效，则某个特定的偏相关系数的自由度是基于在任何
零阶相关计算中使用的最小个案数。

用spss相关性分析，相关系数是0.271相关性怎么样

表6变量间相关性分析AreaDISLN（DLI）t-1LN(Bac)t-1LN（Size）t-1LN(Donation)tLN(Donation)tPearson相关性.463**.561**-.225**.788**.650**1显著性（双侧）.000.000.003.000.000N169...

表6 变量间相关性分析

Area
DIS
LN（DLI）t-1
LN(Bac)t-1
LN（Size）t-1
LN(Donation)t
LN(Donation)t
Pearson 相关性
.463**
.561**
-.225**
.788**
.650**
1
显著性（双侧）
.000
.000
.003
.000
.000

N
169
169
169
169
169
169
**. 在 .01 水平（双侧）上显著相关。
这个相关性怎么解释，还有那个显著性怎么解释啊 展开

0.271属于低相关，这是分析相关系数的大小。

相关系数：

1、0.8-1.0：极强相关。

2、0.6-0.8：强相关。

3、0.4-0.6：中等程度相关。

4、0.2-0.4：弱相关。

5、0.0-0.2：极弱相关或无相关。

相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

简单相关系数：又叫相关系数或线性相关系数，一般用字母r 表示，用来度量两个变量间的线性关系。

定义式：

其中，Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差。

复相关系数：又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如，某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。

典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。

生活示例：

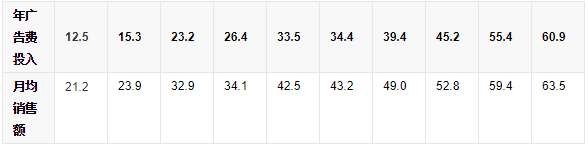
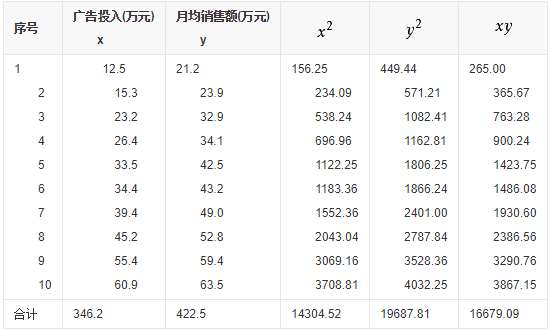
软件公司在全国有许多代理商，为研究它的财务软件产品的广告投入与销售额的关系，统计人员随机选择10家代理商进行观察，搜集到年广告投入费和月平均销售额的数据，并编制成相关表，见表1:

表1：广告费与月平均销售额相关表 单位：万元

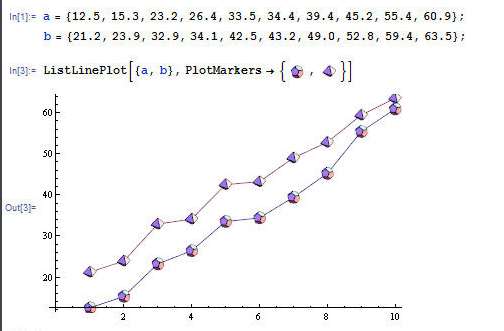
参照表1，可计算相关系数如表2：

相关系数为0.9942，说明广告投入费与月平均销售额之间有高度的线性正相关关系。

扩展资料：

相关系数缺点：

需要指出的是，相关系数有一个明显的缺点，即它接近于1的程度与数据组数n相关，这容易给人一种假象。因为，当n较小时，相关系数的波动较大，对有些样本相关系数的绝对值易接近于1；当n较大时，相关系数的绝对值容易偏小。

特别是当n=2时，相关系数的绝对值总为1。因此在样本容量n较小时，我们仅凭相关系数较大就判定变量x与y之间有密切的线性关系是不妥当的。

相关系数性质：

这里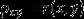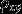，  ，  是一个可以表征  和  之间线性关系紧密程度的量。它具有两个性质：

（1） 

（2）  的充要条件是，存在常数a，b，使得 

由性质衍生：

a. 相关系数定量地刻画了 X 和 Y的相关程度，即 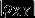 越大，相关程度越大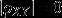；  对应相关程度最低；

b. X 和Y 完全相关的含义是在概率为1的意义下存在线性关系，于是 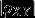 是一个可以表征X 和Y 之间线性关系紧密程度的量。

当 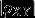 较大时，通常说X 和Y相关程度较好；当  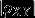较小时，通常说X 和Y相关程度较差；当X和Y不相关，通常认为X和Y之间不存在线性关系，但并不能排除X和Y之间可能存在其他关系。

参考资料：百度百科-相关系数

参考资料：百度百科-spss

spss相关性分析

SPSS（Statistical Product and Service Solutions），“统计产品与服务解决方案”软件。最初软件全称为“社会科学统计软件包”（SolutionsStatistical Package for the Social Sciences），但是随着SPSS产品服务领域的扩大和服务深度的增加，SPSS公司已于2000年正式将英文全称更改为“统计产品与服务解决方案”，这标志着SPSS的战略方向正在做出重大调整。SPSS为IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品及相关服务的总称，有Windows和Mac OS X等版本。 1984年SPSS总部首先推出了世界上第一个统计分析软件微机版本SPSS/PC+，开创了SPSS微机系列产品的开发方向，极大地扩充了它的应用范围，并使其能很快地应用于自然科学、技术科学、社会科学的各个领域。世界上许多有影响的报刊杂志纷纷就SPSS的自动统计绘图、数据的深入分析、使用方便、功能齐全等方面给予了高度的评价。

液晶电视什么品牌好

头脑特工队免费完整版