曲谱自学网今天精心准备的是《正十七边形尺规作图》，下面是详解！

高斯是怎样画出正17边形的？

高斯是怎样画出正17边形的？...

高斯是怎样画出正17边形的？

做法步骤如下：

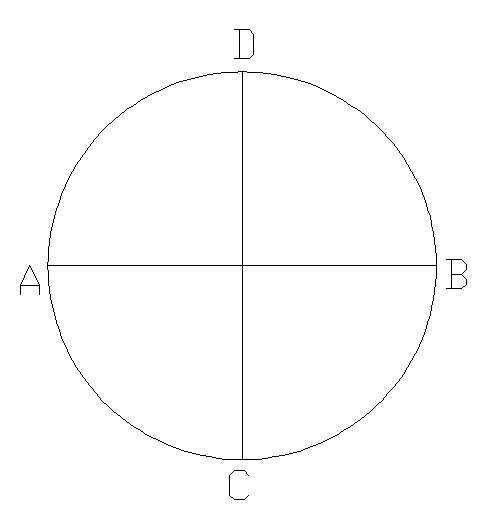
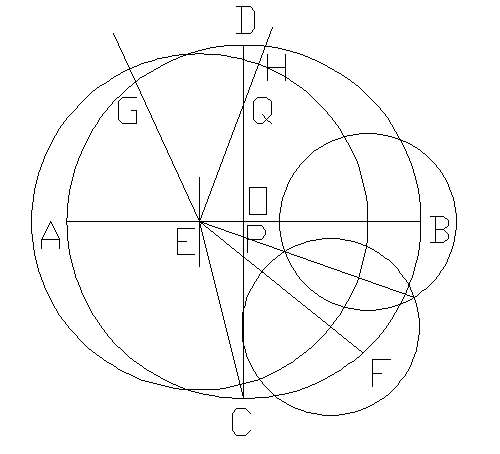
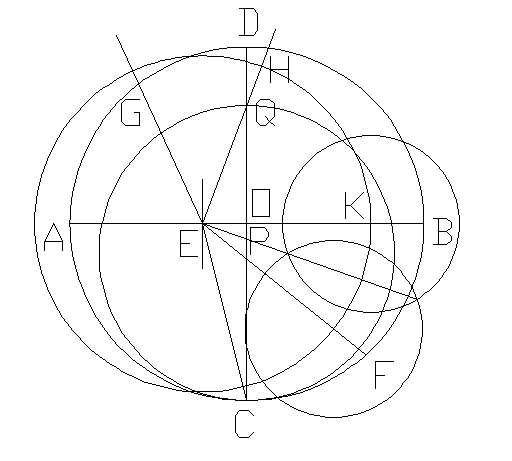
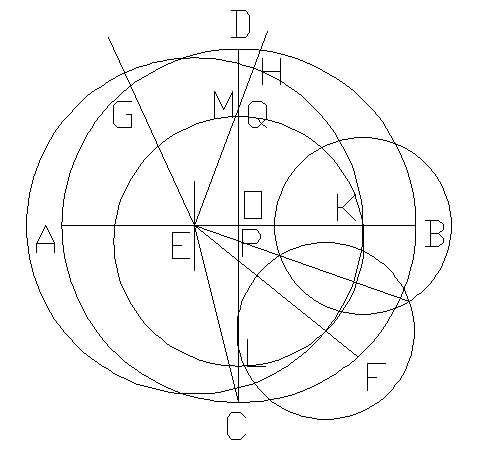
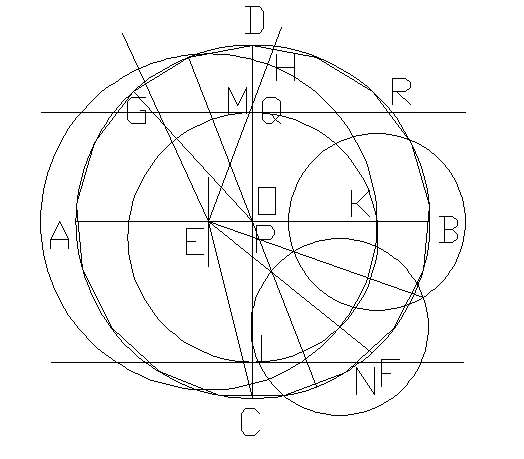
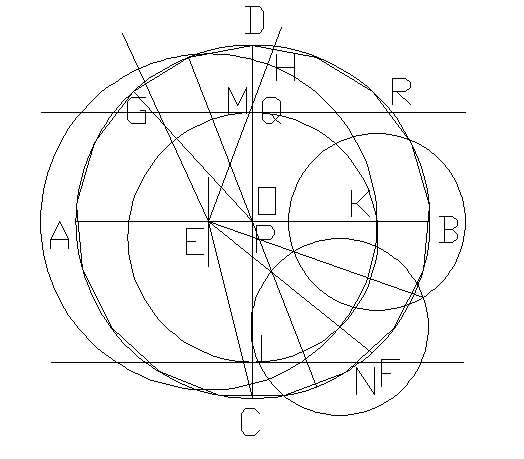
（1）给一圆O，作两垂直的直径AB、CD：

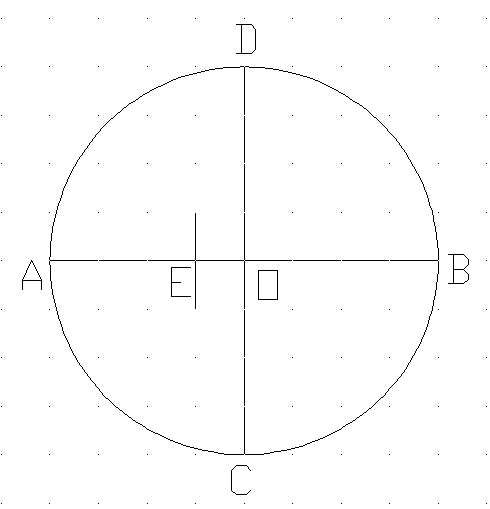
（2）在OA上作E点使OE=1/4AO，连结CE,：

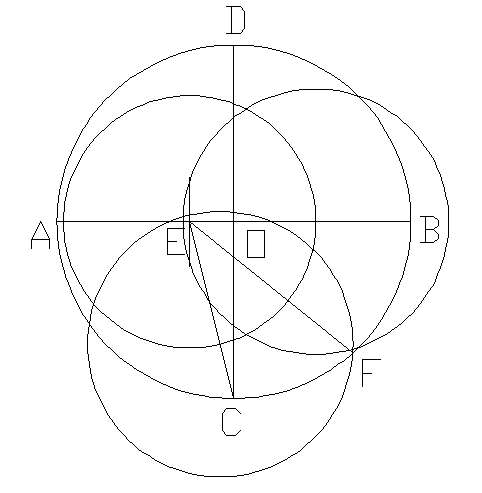
（3）作∠CEB的平分线EF：

（4）作∠FEB的平分线EG，交CO于P：

（5）作∠GEH=45°，交CD于Q：

（6）以CQ为直径作圆，交OB于K：

（7）以P为圆心,PK为半径作圆.交CD于L、M：

（8）分别过M、L作CD的垂线，交圆O于N、R：

（9）作弧NR的中点S，以SN为半径将圆O分成17等份：

最后几何作图如下：

简易作法

因为360°/17≈21°10′ ，利用sinA 21°6′=0.3600可得近似角。

用该方法作正十七边形总误差为17*4′=68′，在不要求十分精确的情况下还是可行的。

作法如下：

1. 先画一条直线，用圆规在上面截取5条相等线段，(尽量越短越好),再截取之前四条线段的和，接续之前画的线段。这样，如果每条小线段算作0.1的话，那么整条线段就是1.8。

2. 用圆规截取之前5条小线段的长，画5次，这样这条线段就是5。1.8/5=0.36。准备工作完毕！

3. 另作一条直线，作垂线，1.8的线段作为对边，5的线段作为斜边，那个最小的锐角即是近似的360°/17的角。以其顶点为圆心，重复作角直至闭合。画一大圆，连接其与17条射线的交点，即可。

扩展资料

画正多边形，就是把圆平均n等份，通过代数计算，弦长的半径的多少倍，再用尺规作图把圆n等份，这样每个相邻的点连接起来，就是正n边形，必须利用圆这个图形。

正十七边形是指几何学中有17条边及17只角的正多边形。正十七边形的每个内角约为158.823529411765°，其内角和为2700°，有119条对角线。

最早的十七边形画法创造人是高斯

1801年数学家高斯证明：如果费马数k为质数，那么就可以用直尺和圆规将圆周k等分。但是，高斯本人并没有用尺规做出正十七边形，事实上，完成证明之后正十七边形的做法对数学研究者是显而易见的。第一个真正的正十七边形尺规作图法是在1825年由约翰尼斯·厄钦格（Johannes Erchinger）给出

最早发现其形状可用尺规作图法作出的是高斯。

参考资料来源： 正十七边形作发

尺规作图正十七边形，做法的视频。

尺规作图正十七边形，做法的视频，下面是图片，看不懂，要视频的，最好有解说。谢谢！速求!邮箱：1020272037@qq.com或者链接...

尺规作图正十七边形，做法的视频，下面是图片，看不懂，要视频的，最好有解说。谢谢！速求!
邮箱：1020272037@qq.com
或者链接

• 

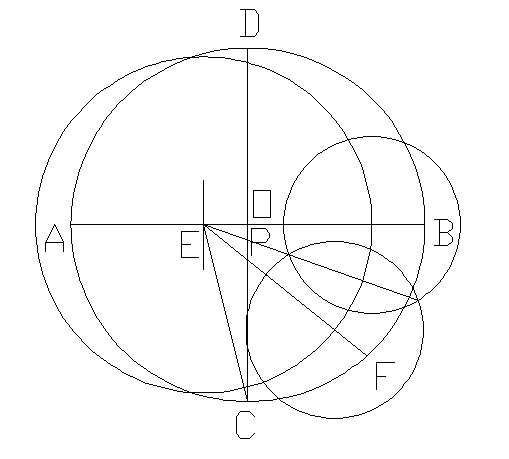
我看了一些视频，其实还不如用图讲得清楚。你这张图把太多中间步骤都画上去，太乱了所以不容易看，我给你一张简洁的图，保证你能看懂。

步骤：

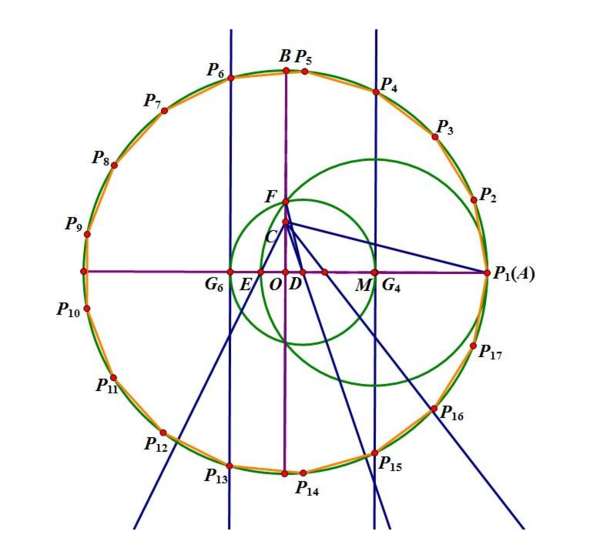
1、以O为圆心作一个圆，在圆周上任取一点P1作为正十七边形的第一个顶点；

2、画出直径OP1，并作另一条半径OB垂直于OP1；

3、把OB四等分，得到J点；

4、连接JP1，作角OJP1的四等分线JE；

5、作一个45度角EJF；

6、以FP1为直径作半圆，交OB于K点；

7、以E为圆心，EK为半径作半圆，交直径OP1于N4点；

8、从N4点作OP1的垂线，这条垂线跟圆的交点就是正十七边形的第四个顶点P4；

9、有了P4剩下的顶点就都可以找到了，很容易，以P1P4为半径去截圆周，就依次得到全部顶点。

这个作图跟你给的那个本质上是一样的，它最早是Richmond于1893年提出的，非常巧妙的一个作图。

扩展

太好玩了，真神奇，good！
还有你这个图是怎么画的，，网上找的还是用软件画的，有的什么软件？

补充

图是网上找的，来自世界上最大最权威的数学百科网站Wolfram MathWorld，一切数学名词都可以在这里查到。
正十七边形：http://mathworld.wolfram.com/Heptadecagon.html
著名的数学工具软件mathematica也是Wolfram开发的，所以他们这个网站上的图可能都是用mathematica画的。
http://www.wolfram.com/mathematica/index.zh.html

请教如何用尺规作图画一个正十七边形？请详细说明...

好难啊，不过我是天才哦\r\n步骤一： \r\n给一圆O，作两垂直的直径OA、OB， \r\n作C点使OC＝1\\/4OB， \r\n作D点使∠OCD＝1\\/4∠OCA， \r\n作AO延长线上E点使得∠DCE＝45度。 \r\n\r\n步骤二： \r\n作AE中点M，并以M为圆心作一圆过A点，此圆交OB于F点， \r\n再以D为圆心，作一圆过F点，此圆交直线OA于G4和G6两点。 \r\n\r\n步骤三： \r\n过G4作OA垂直线交圆O于P4， \r\n过G6作OA垂直线交圆O于P6， \r\n则以圆O为基准圆，A为正十七边形之第一顶点P4为第四顶点，P6为第六顶点。 \r\n以1\\/2弧P4P6为半径，即可在此圆上截出正十七边形的所有顶点。 \r\n\r\n\r\n如果能帮你请多给点分

请问这正十七边形的尺规作图过程gif图片是用什么软...

如图，显然，制作这图片的人不仅是个GIF高手，而且是个数学高手。我可以制作简单的GIF图片，但对这图百思不得其解，不知道是用什么软件制作的（或者综合用几种软件来制作），具体怎么...

如图，显然，制作这图片的人不仅是个GIF高手，而且是个数学高手。我可以制作简单的GIF图片，但对这图百思不得其解，不知道是用什么软件制作的（或者综合用几种软件来制作），具体怎么制作？回答好的必定重重追加！
关键是，用flash无法精确画出圆（精确定位圆心和半径），无法精确画出直线（精确经过指定两点的直线），圆规的两脚张开不同角度图片也必须一张张手工画出来吗？还是用flash可以自动生成？（这图圆规画的非常好应该是用什么软件生成的） 展开

• 

这是一张gif格式的图片，圆规是一张预先制作好的图片。制作方法很多，可以使用ae、ps、u5、flash等。你看见的线条的游动，是事先设计好的动画（建立关键帧），再将圆规放在上面做样子，类似于用笔写字的动画。
用ae制作这样的动画比较简单，制作好直线、曲线游动，再把圆规图片的两个角按曲线或直线的轨迹移动（建立关键帧），输出格式为gif。flash等做法于此基本相同

困扰了数学家两千年之久的正十七边形尺规作图问题...

最早的十七边形画法创造人是高斯【1801年数学家高斯证明：如果费马数k为质数，那么就可以用直尺和圆规将圆周k等分.但是，高斯本人实际上并不会做正十七边形。第一个真正的正十七边形尺规作图法直到1825年才由约翰尼斯·厄钦格（Johannes Erchinger）给出.】^[1]  。高斯（1777─1855年）德国数学家、物理学家和天文学家。高斯在童年时代就表现出非凡的数学天才。年仅三岁，就学会了算术，八岁因运用等差数列求和公式而深得老师和同学的钦佩。大学二年级时得出正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件。解决了两千年来悬而未决的难题，1799年以代数基本定理的四个漂亮证明获博士学位。高斯的数学成就遍及各个领域，在数学许多方面的贡献都有着划时代的意义。并在天文学，大地测量学和磁学的研究中都有杰出的贡献

 

因为360°/17≈21°10′ ,利用sinA 21°6′=0.3600可得近似角。用该方法作正十七边形总误差为17*4′=68′，在不要求十分精确的情况下还是可行的。作法如下：1.先画一条直线，用圆规在上面截取5条相等线段，(尽量越短越好),再截取之前四条线段的和，接续之前画的线段。这样，如果每条小线段算作0.1的话，那么整条线段就是1.8。2.用圆规截取之前5条小线段的长，画5次，这样这条线段就是5。1.8/5=0.36。准备工作完毕！3.另作一条直线，作垂线，1.8的线段作为对边，5的线段作为斜边，那个最小的锐角即是近似的360°/17的角。以其顶点为圆心，重复作角直至闭合。画一大圆，连接其与17条射线的交点，即可。

正十七边形尺规作图怎么做

数学家高斯的正十七边形的尺规作图，数学老师出的，好难...

数学家高斯的正十七边形的尺规作图，数学老师出的，好难

步骤一： 给一圆O，作两垂直的直径OA、OB， 在OB上作C点使OC＝1/4OB， 作D点使∠OCD＝1/4∠OCA 作AO延长线上E点使得∠DCE＝45度 步骤二： 作AE中点M，并以M为圆心作一圆过A点， 此圆交OB于F点，再以D为圆心，作一圆 过F点，此圆交直线OA于G4和G6两点。 步骤三： 过G4作OA垂直线交圆O于P4， 过G6作OA垂直线交圆O于P6， 则以圆O为基准圆，A为正十七边形之第一顶点， P4为第四顶点，P6为第六顶点。 以1/2弧P4P6为半径，即可在此圆上截出正十七边形的所有顶点。 备注一 一个正质数多边形可以用标尺作图的充分和必要条件是，该多边形的边数必定是一个费马质数。换句话说，只有正三边形、正五边形、正十七边形、正257边形和正63357边形可以用尺规作出来，其它的正质数多边形就不可以了。（除非我们再发现另一个费马质数。） 备注二 黎西罗给出了正257边形的尺规作法，写满了整整80页纸。盖尔梅斯给出了正63357边形的尺规作法，此手稿整整装满了一只手提箱，现存于德国哥廷根大学。这是有史以来最繁琐的尺规作图。 备注三 正十七边形的尺规作图存在之证明: 设正17边形中心角为a,则17a=360度,即16a=360度-a 故sin16a=-sina,而 sin16a=2sin8acos8a=2方sin4acos4acos8a=2的4次方sinacosacos2acos4acos8a 因sina不等于0,两边除之有: 16cosacos2acos4acos8a=-1 又由2cosacos2a=cosa+cos3a等,有 2(cosa+cos2a+…+cos8a)=-1 注意到 cos15a=cos2a,cos12a=cos5a,令 x=cosa+cos2a+cos4a+cos8a y=cos3a+cos5a+cos6a+cos7a 有: x+y=-1/2 又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a) =1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a) 经计算知xy=-1 又有 x=(-1+根号17)/4,y=(-1-根号17)/4 其次再设: x1=cosa+cos4a,x2=cos2a+cos8a y1=cos3a+cos5a,y2=cos6a+cos7a 故有x1+x2=(-1+根号17)/4 y1+y2=(-1-根号17)/4 解之可有: (您自己解解吧~~~~) 最后,由cosa+cos4a=x1,cosacos4a=(y1)/2 可求cosa之表达式,它是数的加减乘除平方根的组合, 故正17边形可用尺规作出。

正十七边形怎么尺规作图？

正十七边形怎么尺规作图？顺便讲一下卡尔·弗里德里希·高斯作出来的故事...

正十七边形怎么尺规作图？顺便讲一下卡尔·弗里德里希·高斯作出来的故事

高斯只是证明了尺规作图可以作出正十七边形。。。他本身没给出方法
要知道怎么昨天 网上去搜一下 还是比较复杂的

正十七边形尺规作图这样怎么画

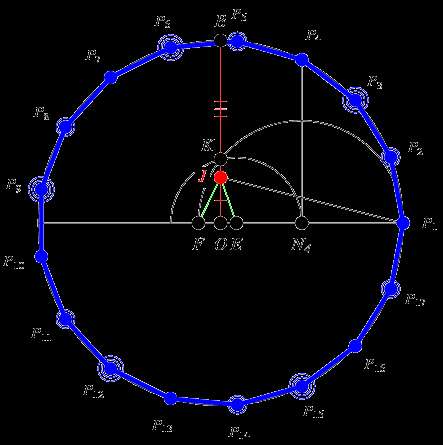
我在维基百科找到一幅gif的画正十七边形的图片，上面画的很详细，但看不出原点和半径，谁能说一下这种话发的详细步骤。图片地址：http://zh.wikipedia.org/w/index.php?title=File:He...

我在维基百科找到一幅gif的画正十七边形的图片，上面画的很详细，但看不出原点和半径，谁能说一下这种话发的详细步骤。图片地址：http://zh.wikipedia.org/w/index.php?title=File:HeptadecagonConstructionAni.gif&variant=zh-cn 展开

我58岁了，只有小学文化，不会在电脑上作图，只好用文字给你描述了。请原谅！ 正多边形的画法： 1.作一互相垂直的十字线，把交叉点称为o点。 2.以o点为圆心作圆，圆与十字线分别相交于a、b、c、d点。（把相当于时钟12点的位置叫做a点，6点的位置叫做b点，9点的位置叫做c点，3点的位置叫做d点）。 3.等分线段ab（需要作正几边形就把ab等分成相应的份数），咱把线段ab被等分后得到的点依次称为a、1、2、3......b点）。 4.以b点为圆心，ba为半径作圆弧，与cd的延长线交于f点。 5.连接f、2两点，其延长线与圆周交于g点，ag就是内接正多边形的边长。（无论你需要画正几边形，都是连接f、2两点）。 6.用分规在圆周上画出正多边形的各顶点，再用三角板画出各边线，这样你所要的正多边形就完成了。 这种画法叫做“过2点相交法”；应用这种方法，可以画出5边及以上任意正多边形来。

正十七边形有什么用？

高斯发现的，可以用在什么领悟？都可以有什么帮助？...

高斯发现的，可以用在什么领悟？都可以有什么帮助？

不预先定义“有用”，很难回答“有什么用”的。

尺规作图，是由来已久的一个数学课题。

做一个正n变形，要求只用不带刻度的直尺和圆规，是不是对任意的n都成立？——这个问题困惑了人们很多年，直到高斯证明了，若费马数Fn是素数，则正F(n)边形可用尺规作图完成——同时，高斯给出了正17边形的尺规作图步骤。

所谓费马数，指的是形如F(n)=[2^(2^n)]+1这样的整数，比如很容易算出：F(0)=2^(2^0)+1=3，F(1)=2^(2^1)+1=5，F(2)=17，F(3)=257，...因此17是第二个费马数，而且是素数，按照高斯给出的定理，是能尺规作图的。

“领悟”这个词很个人化，因人而异吧，比如，从中可以看见数学的美丽，数字的奇妙。

至于说到“帮助”，大概属于精神领域的形而上内容了，喜欢，就有欣喜，对个人的精神世界算是有所裨益吧。

怎么用尺规作图 做成正十七边形

1.将圆的竖直直径AX进行17等分，得到16个等分点；
2.以N点为圆心，以AX为半径画弧，与水平直径的延长线交与N1、N2两点；
3.把N1、N2两点分别与2、4、6、8、10、12、14、16相连，并将连线延长，与圆周相交，得到交点B、J、C、K、D、L、E、M、F、N、G、O、H、P、I、Q。
4.把A、B、C、D、E、F、G、H、I、J、K、L、M、N、O、P、Q17个点按顺序连接起来，得到圆的内接十七边形
圆的内接正n边形的作图顺序和上面这个时期变形的作图方法都差不多

张国荣最后一部电影

win7查看隐藏文件