曲谱自学网今天精心准备的是《三角形相似的判定定理》，下面是详解！

相似三角形判定方法

越多越好，越详细越好．...

越多越好，越详细越好．

相似三角形的判定：

定理1、两角分别对应相等的两个三角形相似。

定理2、两边成比例且夹角相等的两个三角形相似。

定理3、三边成比例的两个三角形相似。

定理4、一条直角边与斜边成比例的两个直角三角形相似。

根据以上判定定理，可以推出下列结论：

推论1、三边对应平行的两个三角形相似。 

推论2、一个三角形的两边和三角形任意一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。

扩展资料：

相似三角形的特例：

1、两个全等的三角形

（全等三角形是特殊的相似三角形，相似比为1：1）

2、两个等腰三角形

（两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。）

3、两个等边三角形

(两个等边三角形，三个内角都是60度，且边边相等，所以相似)

4、直角三角形中由斜边的高形成的三个三角形

参考资料来源：百度百科-相似三角形

相似三角形的判定定理

相似三角形的判定定理:
(1)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,(简叙为两角对应相等两三角形相似).
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为:两边对应成比例且夹角相等,两个三角形相似.)
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(简叙为:三边对应成比例,两个三角形相似.)

三角形相似的判定定理是什么时候学

好像是初二。
相似三角形的性质定理：
(1)相似三角形的对应角相等；
(2)相似三角形的对应边成比例；
(3)相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比；
(4)相似三角形的面积比等于相似比的平方；
(5)平行三角形一边的直线和其他两边所构成的三角形与原三角形相似，如果两个三角形对应边的比相等,这2个三角形也可以说明相似；
(6)要证明△ABC∽△A B C全等要把他们的关系联系起来.相似三角形的传递性：如果△ABC∽△A¹B¹C¹，△A¹B¹C¹∽△A²B²C²，那么△ABC∽ΔA²B²C²

相似三角形判定定理有哪些（全部）？

判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。（简叙为：两角对应相等，两个三角形相似。）（AA）

判定定理2：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两个三角形相似。（简叙为：两边对应成比例且夹角相等，两个三角形相似。）（SAS）

判定定理3：如果两个三角形的三组对应边成比例，那么这两个三角形相似。（简叙为：三边对应成比例，两个三角形相似。）（SSS）
　　判定定理4：两个三角形三边对应平行，则个两三角形相似。（简叙为：三边对应平行，两个三角形相似。）

判定定理5：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。（简叙为：斜边与直角边对应成比例，两个直角三角形相似。）（HL）

判定定理6：如果两个三角形全等，那么这两个三角形相似（相似比为1：1）（简叙为：全等三角形相似。
亲记得哦

更多扩展补充

扩展

全等的有哪些？

补充

SSS,SAS,ASA,AAS,HL 
也就是 
1、三组对应边分别相等的两个三角形全等(简称SSS)。 

2、有两边及其夹角对应相等的两个三角形全等(SAS)。 

3、有两角及其夹边对应相等的两个三角形全等(ASA) 

注:S是边的英文缩写,A是角的英文缩写 

由3可推到 

4、有两角及一角的对边对应相等的两个三角形全等(AAS) 

5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL)

亲呗😘😘

如何证明相似三角形判定定理（三条） 1.两角对应相...

如何证明相似三角形判定定理（三条）1.两角对应相等的像个三角形相似2.三边对应成比例的两个三角形相似3.两边对应成比例及其夹角相等的两个三角形相似请证明（用公理和已证定理）...

如何证明相似三角形判定定理（三条）
1.两角对应相等的像个三角形相似
2.三边对应成比例的两个三角形相似
3.两边对应成比例及其夹角相等的两个三角形相似

请证明（用公理和已证定理）

相似三角形的认识
　　对应角相等，对应边成比例的两个三角形叫做相似三角形。（similar triangles）。
　　互为相似形的三角形叫做相似三角形
相似三角形的判定方法
　　根据相似图形的特征来判断。（对应边成比例，对应角相等）
　　1.平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似；
　　（这是相似三角形判定的引理，是以下判定方法证明的基础。这个引理的证明方法需要平行线分线段成比例的证明）
　　2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似；
　　
　　3.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似；
　　
　　4.如果两个三角形的三组对应边的比相等,那么这两个三角形相似；
　　
　　
绝对相似三角形

　　1.两个全等的三角形一定相似。
　　
　　2.两个等腰直角三角形一定相似。
　　
　　3.两个等边三角形一定相似。
　　
　　直角三角形相似判定定理
　　1.斜边与一条直角边对应成比例的两直角三角形相似。
　　2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。
　　射影定理
　　三角形相似的判定定理推论
　　推论一：顶角或底角相等的那个的两个等腰三角形相似。
　　推论二：腰和底对应成比例的两个等腰三角形相似。
　　推论三：有一个锐角相等的两个直角三角形相似。
　　推论四：直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
　　推论五：如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。
　　推论六：如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。
相似三角形的性质
　　1.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。
　　2.相似三角形周长的比等于相似比。
　　3.相似三角形面积的比等于相似比的平方。
相似三角形的特例
　　能够完全重合的两个三角形叫做全等三角形。（congruent triangles）
　　全等三角形是相似三角形的特例。全等三角形的特征：
　　1.形状完全相同，相似比是k=1。
　　全等三角形一定是相似三角形，而相似三角形不一定是全等三角形。
　　因此，相似三角形包括全等三角形。
　　全等三角形的定义
　　能够完全重合的两个三角形称为全等三角形。（注：全等三角形是相似三角形中的特殊情况）
　　当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。
　　由此，可以得出：全等三角形的对应边相等，对应角相等。
　　(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；
　　(2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；
　　(3)有公共边的，公共边一定是对应边；
　　(4)有公共角的，角一定是对应角；
　　(5)有对顶角的，对顶角一定是对应角；
　　三角形全等的判定公理及推论
　　1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)，这一条也说明了三角形具有稳定性的原因。
　　2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。
　　3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。
　　由3可推到
　　4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)
　　5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边，直角边”)
　　所以，SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
　　注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。
　　A是英文角的缩写(angle)，S是英文边的缩写(side)。
　　全等三角形的性质
　　1、全等三角形的对应角相等、对应边相等。
　　2、全等三角形的对应边上的高对应相等。
　　3、全等三角形的对应角平分线相等。
　　4、全等三角形的对应中线相等。
　　5、全等三角形面积相等。
　　6、全等三角形周长相等。
　　7、三边对应相等的两个三角形全等。（SSS)
　　8、两边和它们的夹角对应相等的两个三角形全等。(SAS)
　　9、两角和它们的夹边对应相等的两个三角形全等。(ASA)
　　10、两个角和其中一个角的对边对应相等的两个三角形全等。(AAS)
　　11、斜边和一条直角边对应相等的两个直角三角形全等。(HL)
　　全等三角形的运用
　　1、性质中三角形全等是条件，结论是对应角、对应边相等。 而全等的判定却刚好相反。
　　2、利用性质和判定，学会准确地找出两个全等三角形中的对应边与对应角是关键。在写两个三角形全等时，一定把对应的顶点，角、边的顺序写一致，为找对应边，角提供方便。
　　3，当图中出现两个以上等边三角形时，应首先考虑用SAS找全等三角形。
　　4、用在实际中，一般我们用全等三角形测等距离。以及等角，用于工业和军事。有一定帮助。
　　全等三角形做题技巧
　　一般来说考试中线段和角相等需要证明全等。
　　因此我们可以来采取逆思维的方式。
　　来想要证全等，则需要什么
　　另一种则要根据题目中给出的已知条件，求出有关信息。
　　然后把所得的等式运用（AAS/ASA/SAS/SSS/HL）证明三角形全等。
　　位似
　　概念：相似且对应顶点的连线相交于一点，对应边互相平行的两个图形叫做位似。
　　位似一定相似但相似不一定位似~

扩展

？

初中数学~证明三角形相似的相关定理~

91、相似三角形判定定理1两角对应相等，两三角形相似（ASA）92、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93、判定定理2两边对应成比例且夹角相等，两三角形相似（S...

91、相似三角形判定定理1 两角对应相等，两三角形相似（ASA）
92、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
93、判定定理2 两边对应成比例且夹角相等，两三角形相似（SAS）
94、判定定理3 三边对应成比例，两三角形相似（SSS）

请问除了这四个还有其他的吗？
括号里的简写对吗？直角三角形的简写是什么？

感谢！ 展开

1、边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
2、角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等
3、推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等
4、边边边公理(SSS) 有三边对应相等的两个三角形全等
5、斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等

扩展

汗，您这个是证明全等的，我要证明相似的。。。囧

补充

1 定理 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似 
2 相似三角形判定定理1 两角对应相等，两三角形相似（ASA） 
3 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似 
4 判定定理2 两边对应成比例且夹角相等，两三角形相似（SAS） 
5 判定定理3 三边对应成比例，两三角形相似（SSS） 
6 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似

证明三角形相似的几个定理。

相似三角形的判定定理：
(1)平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似；
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为：两边对应成比例且夹角相等，两个三角形相似.)；
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似
(简叙为:三边对应成比例，两个三角形相似.)；
(4)如果两个三角形的两个角分别对应相等（或三个角分别对应相等），则有两个三角形相似
(简叙为两角对应相等，两个三角形相似.).
直角三角形相似的判定定理：
(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似；
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似.

相似三角形的判定定理

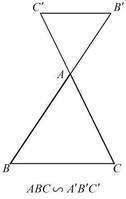
对应角相等，对应边成比例的两个三角形叫做相似三角形。互为相似形的三角形叫做相似三角形。图中，若B'C'//BC，那么角B=角B'，角BAC=角C'A'B'，是对顶角，那么我们就说△ABC∽△AB'C'

三角形的相似怎么学

相似三角形的定义：
对应角相等、对应边成比例的两个三角形叫做相似三角形.
如果三边分别对应A,B,C和a,b,c：那么：
A/a=B/b=C/c
即三边边长对应比例相同.
【这是初中数学知识】
平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似.（这是相似三角形判定的定理,是以下判定方法证明的基础.这个引理的证明方法需要平行线与线段成比例的证明）
定义判定
对应角相等,对应边成比例的两个三角形叫做相似三角形.
判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似（AA）
判定定理2：如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似（SAS）
判定定理3：如果两个三角形的三组对应边成比例,那么这两个三角形相似（SSS）
判定定理4：两三角形三边对应平行,则两三角形相似.
判定定理5：两个直角三角形中,斜边与直角边对应成比例,那么两三角形相似.
其他判定：由角度比转化为线段比：h1/h2=Sabc
判定定理基本判定
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.(简叙为：两边对应成比例且夹角相等,两个三角形相似.)
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.(简叙为：三边对应成比例,两个三角形相似.)

三角形相似的判定定理

三角分别相等，三边成比例的两个三角形叫做相似三角形(similar triangles) 相似三角形是几何中重要的证明模型之一，是全等三角形的推广。全等三角形可以被理解为相似比为1的相似三角形。相似三角形其实是一套定理的集合，它主要描述了在相似三角形是几何中两个三角形中，边、角的关系。

乳腺增生怎么治最好

第一次坐飞机常见尴尬