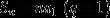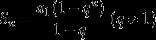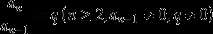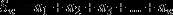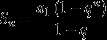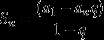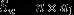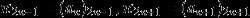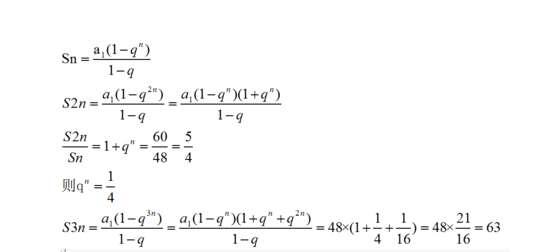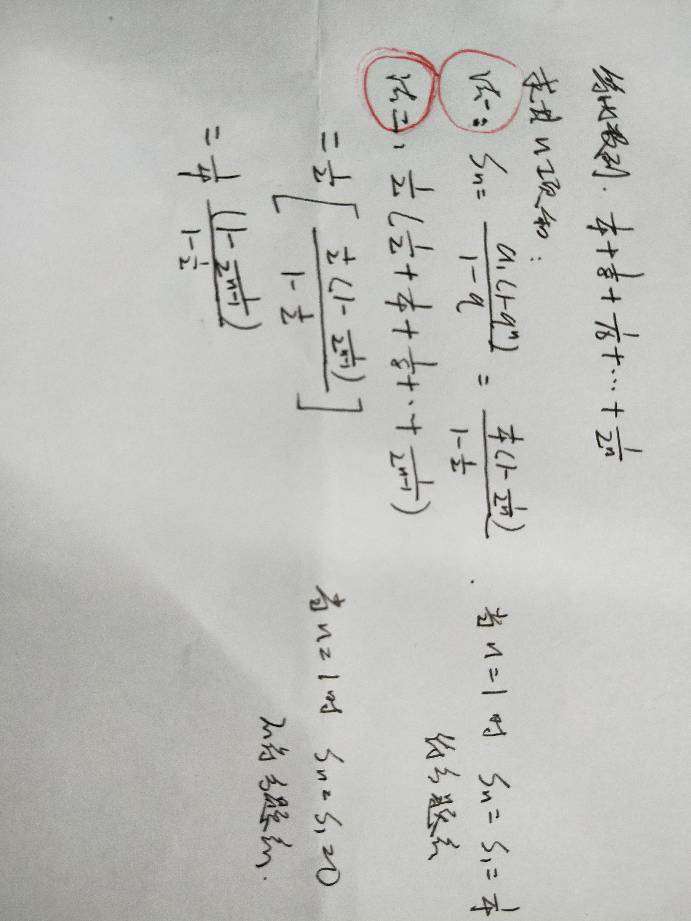等比数列的前n项和
曲谱自学网今天精心准备的是《等比数列的前n项和》,下面是详解!
等比与等差数列前N项和公式?
1、等比数列求和公式:
2、等差数列求和公式:
若一个等差数列的首项为  ,末项为
,末项为 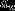 那么该等差数列和表达式为:
那么该等差数列和表达式为: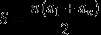
即(首项+末项)×项数÷2。
扩展资料
等比数列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列,常用G、P表示。这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),等比数列a1≠ 0。其中{an}中的每一项均不为0。注:q=1 时,an为常数列。
等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。这个常数叫做等差数列的公差,公差常用字母d表示。
参考资料:百度百科-等比数列 百度百科-等差数列
等比数列前n项和公式
等比数列前n项和公式:Sn =a1(1-q^n)/(1-q)。
推导如下:
因为an = a1q^(n-1)
所以Sn = a1+a1*q^1+...+a1*q^(n-1) (1)
qSn =a1*q^1+a1q^2+...+a1*q^n (2)
(1)-(2)注意(1)式的第一项不变。
把(1)式的第二项减去(2)式的第一项。
把(1)式的第三项减去(2)式的第二项。
以此类推,把(1)式的第n项减去(2)式的第n-1项。
(2)式的第n项不变,这叫错位相减,其目的就是消去这此公共项。
于是得到
(1-q)Sn = a1(1-q^n)
即Sn =a1(1-q^n)/(1-q)。
扩展资料:
等比数列前n项和性质
①若 m、n、p、q∈N,且m+n=p+q,则aman=apaq。
②在等比数列中,依次每 k项之和仍成等比数列。
③若m、n、q∈N,且m+n=2q,则am×an=(aq)^2。
④ 若G是a、b的等比中项,则G²=ab(G ≠ 0)。
⑤在等比数列中,首项a1与公比q都不为零。
⑥在数列{an}中每隔k(k∈N*)取出一项,按原来顺序排列,所得新数列仍为等比数列且公比为q^(k+1)。
⑦当数列{an}使各项都为正数的等比数列,数列{lgan}是lgq的等差数列。
参考资料来源:百度百科-等比数列求和公式
等比数列前n项和公式有两个,第二个是什么?
分析如下:
等比数列前n项和公式第二个是
①当q≠1时,
或
②当q=1时,
记
,则有
拓展资料:
1、等比数列公式就是在数学上求一定数量的等比数列的和的公式。另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列。
2、如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。
若通项公式变形为 (n∈N*),当q>0时,则可把
(n∈N*),当q>0时,则可把 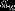 看作自变量n的函数,点(n,
看作自变量n的函数,点(n, 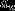 )是曲线
)是曲线
从等比数列的定义、通项公式、前n项和公式可以推出: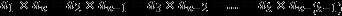 ,k∈{1,2,…,n}
,k∈{1,2,…,n}
等比中项:当r满足p+q=2r时,那么则有 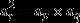 ,即
,即 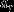 为
为 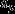 与
与 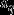 的等比中项。
的等比中项。
(资料来源:百度百科:等比数列)
等比数列前n项和的公式是怎么推导出来的
这样来的:
Sn=a1+a1q+a1q²+......+a1q^(n-1)
qSn= a1q+a1q²+......+a1q^(n-1)+a1q^n
两式对应相减得:Sn-qSn=a1-a1q^n
得Sn=a1(1-q^n)/(1-q)
等比数列的前n项和的Sn,S2n,S3n有何关系
等比数列的前n项和 Sn、S2n-Sn、S3n-S2n成等比数列,公比为q^n。
证明如下:
设等比数列{an}的公比为q,
an=a1q^(n-1)
am=a1q^(m-1)
两式相除得an/am=q^(n-m),∴an=amq^(n-m)。
S2n=a1+a2+...+an+a(n+1)+a(n+2)+...+a2n=Sn+(a1q^n+a2q^n+...+anq^n)=Sn+(a1+a2+...+an)q^n=Sn+Snq^n
所以 (S2n-Sn)/Sn=q^n。
同理,S3n=S2n+[a(2n+1)+a(2n+2)+...+a3n]
=S2n[a(n+1)q^n+a(n+2)q^n+...+a2nq^n)
=S2n+[a(n+1)+a(n+2)+...+a2n]q^n
=S2n+[S2n-Sn}q^n 。
所以 (S3n-S2n)/(S2n-Sn)=q^n 。
所以 (S2n-Sn)/Sn=(S3n-S2n)/(S2n-Sn)。
即(S2n-Sn)^2=Sn(S3n-S2n) 。
扩展资料:
等比数列求和公式的性质:
①若 m、n、p、q∈N,且m+n=p+q,则aman=apaq;
②在等比数列中,依次每 k项之和仍成等比数列;
③若m、n、q∈N,且m+n=2q,则am×an=(aq)^2;
④ 若G是a、b的等比中项,则G2=ab(G ≠ 0);
⑤在等比数列中,首项a1与公比q都不为零;
⑥在数列{an}中每隔k(k∈N*)取出一项,按原来顺序排列,所得新数列仍为等比数列且公比为q^(k+1);
⑦当数列{an}使各项都为正数的等比数列,数列{lgan}是lgq的等差数列 。
等比数列前n项和函数特性?
为什么当q≠1且q≠0时,Sn=-Aq的n次方+A?还有为什么A=a1/(1-q)?这是怎么推导出的?...
为什么当q≠1且q≠0时,Sn=-Aq的n次方+A?还有为什么A=a1/(1-q)?这是怎么推导出的?
记忆等比数列前n项和公式
有什么好的的方法记忆这个公式吗?你们上学的时候用的?我实在是背不住了,斜斜了就类似于等差数列的:首项加末项乘以项数。这类的话最好了,还有啊等比求和不是两个公式吗?大家都帮...
有什么好的的方法记忆这个公式吗?你们上学的时候用的?我实在是背不住了,斜斜了
就类似于等差数列的:首项加末项乘以项数。这类的话最好了,还有啊 等比求和不是两个公式吗?大家都帮忙想想,多谢最好还有导出的那个等差求和公式,我就是想死记硬背,这才适合我,多谢了
展开
多背几次就完事了。
q=1时,Sn=na1
q不等于1时,
Sn=a1*(1-q^n)/(1-q)
q=1不多说
q不为1时,你看,分子是1-q^n,分母是1-q,最后再乘以a1就完事了。
顺便提醒一下楼主,要想把公式记熟,最好的办法是做做题,提做多了,公式用多了,自然就熟了。(说实话,长时间不用公式是很容易忘的)
求等比数列前n项和
这2种到底哪个是正确解答...
这2种到底哪个是正确解答
你这个一共是n-1项不是n项。
通项公式是an=1/2^(n+1),所以1/2^n显然是第n-1项
所以求的应该是S(n-1)不是Sn
已知等比数列{an}的前n项和Sn=1/2×3∧(n+1)+c(...
已知等比数列{an}的前n项和Sn=1/2×3∧(n+1)+c(c为常数)若不等式λan≦3+S2n恒成立,则实数λ的最大值是...
已知等比数列{an}的前n项和Sn=1/2×3∧(n+1)+c(c为常数)若不等式λan≦3+S2n恒成立,则实数λ的最大值是
n=1时,a1=S1=½·3²+c=9/2 +c
n≥2时,an=Sn-S(n-1)=(½·3ⁿ⁺¹+c)-(½·3ⁿ+c)=3ⁿ
a2=3²=9,q=a(n+1)/an=3ⁿ⁺¹/3ⁿ=3
要a1是等比数列的项,a2/a1=q
a1=a2/q=9/3=3
9/2 +c=3
c=-3/2
λan≤3+S2n
λ·3ⁿ≤3+½·3²ⁿ⁺¹ -3/2
λ≤½(3ⁿ⁺¹+⅓ⁿ⁻¹)
(3ⁿ⁺²+⅓ⁿ)-(3ⁿ⁺¹+⅓ⁿ⁻¹)
=2(3ⁿ⁺¹-⅓ⁿ)
n≥1,3ⁿ⁺¹≥9,⅓ⁿ≤⅓,因此2(3ⁿ⁺¹-⅓ⁿ)恒>0
即随n增大,½(3ⁿ⁺¹+⅓ⁿ⁻¹)单调递增,要不等式恒成立,只需当n=1时不等式成立
λ≤½(3¹⁺¹+⅓¹⁻¹)
λ≤5
实数λ的最大值是5
等比数列前n项和公式
等比数列通项公式...
等比数列通项公式
q=1时,Sn=na1
q不等于1时,
Sn=a1*(1-q^n)/(1-q)
等比数列通项公式 q=1 an=a1
q不为1时 an=a1*q^(n-1)
等比数列的前n项和

等比数列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列,常用G、P表示。这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),等比数列a1≠ 0。其中{an}中的每一项均不为0。注:q=1 时,an为常数列。
热门曲谱
 刘德华喊话四大天王合体做节目:他们愿意我 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37
刘德华喊话四大天王合体做节目:他们愿意我 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37 led和节能灯哪个好
led和节能灯哪个好 概括:这道题是贲友颗同学的课后练习题,主要是关于led和节能灯哪个好,指导老师为黎老师。LED节能灯是继紧凑型荧光灯(即普通节能灯...
[详情]分类:知识库时间:14:47 个人所得税税率
个人所得税税率 概括:这道题是蒲值暇同学的课后练习题,主要是关于个人所得税税率,指导老师为阚老师。
题目:个人所得税税率
解:<...[详情]分类:知识库时间:14:51 个税计算方法
个税计算方法 概括:这道题是文缘卣同学的课后练习题,主要是关于个税计算方法,指导老师为惠老师。负所得税制度的意义财税部门出台了给予弱势群...
[详情]分类:知识库时间:14:51 李光洁宣布结婚 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37
李光洁宣布结婚 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37 什么可以美白牙齿
什么可以美白牙齿 概括:这道题是贡泼俊同学的课后练习题,主要是关于什么可以美白牙齿,指导老师为井老师。冷光美白牙齿顾名思义就是用冷光来美白牙...
[详情]分类:知识库时间:14:58 什么是连带责任
什么是连带责任 概括:这道题是满澄檬同学的课后政治练习题,主要是关于什么是连带责任,指导老师为宦老师。
题目:什么是连带责任
...[详情]分类:知识库时间:14:58 趣头条与江苏卫视达成战略合作 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37
趣头条与江苏卫视达成战略合作 彭于晏带违规水果过海关被罚 据台湾媒体报道,彭于晏7月1日返回台北在松山机场过海关的时候,因为不小心带了水果,被海关查获并罚款3000元台币 。有台湾媒体询问机场工作人...[详情]分类:知识库时间:12:37 利率怎么算
利率怎么算 概括:这道题是从纲凑同学的课后练习题,主要是关于利率怎么算,指导老师为殳老师。银行利率表示一定时期内利息量与本金的比率,通...
[详情]分类:知识库时间:14:58 名贵树种
名贵树种 概括:这道题是山翁灿同学的课后练习题,主要是关于名贵树种,指导老师为谈老师。
题目:名贵树种
解: ...[详情]分类:知识库时间:14:56 埃利斯
埃利斯 概括:这道题是苏似涡同学的课后政治练习题,主要是关于埃利斯,指导老师为裴老师。
题目:埃利斯
解: ...[详情]分类:知识库时间:14:54 差异
差异 概括:这道题是巫唐抖同学的课后练习题,主要是关于差异,指导老师为左老师。暂时性差异是由税收法规与会计准则确认时间或计税基础...
[详情]分类:知识库时间:14:53 平衡梁
平衡梁 概括:这道题是浦晓淖同学的课后练习题,主要是关于平衡梁,指导老师为赵老师。平衡梁为吊装机具的重要组成部分,可用于保持被吊设...
[详情]分类:知识库时间:14:54 建筑图集
建筑图集 概括:这道题是蓟侠位同学的课后政治练习题,主要是关于建筑图集,指导老师为焦老师。《新疆传统建筑图集》是2009年新疆科学技术出...
[详情]分类:知识库时间:14:54 成分分析
成分分析 概括:这道题是颜仑徽同学的课后练习题,主要是关于成分分析,指导老师为戈老师。
题目:成分分析
解: ...[详情]分类:知识库时间:14:56 无坚不摧之力
无坚不摧之力 概括:这道题是路婆掖同学的课后政治练习题,主要是关于无坚不摧之力,指导老师为祁老师。
题目:无坚不摧之力
解:<...[详情]分类:知识库时间:14:54 气垫船原理
气垫船原理 概括:这道题是席洞朴同学的课后练习题,主要是关于气垫船原理,指导老师为毛老师。通风工程是送风、排风、除尘、气力输送以及防、...
[详情]分类:知识库时间:14:54 海狸
海狸 概括:这道题是项筛卦同学的课后练习题,主要是关于海狸,指导老师为钱老师。
题目:海狸
解: ...[详情]分类:知识库时间:14:56 38译码器
38译码器 知识点:《38译码器》 收集:瞿收霉 编辑:桂花
[详情]分类:知识库时间:10:57
本知识点包括:1、38译码器在单片机系统中的作用是什么? 2、求vh... aidma
aidma 知识点:《aidma》 收集:蒯超峦 编辑:栀子花女孩
[详情]分类:知识库时间:12:08
本知识点包括:1、SOV/SOM是什么?AIDMA和AIDAS理论代表什么...