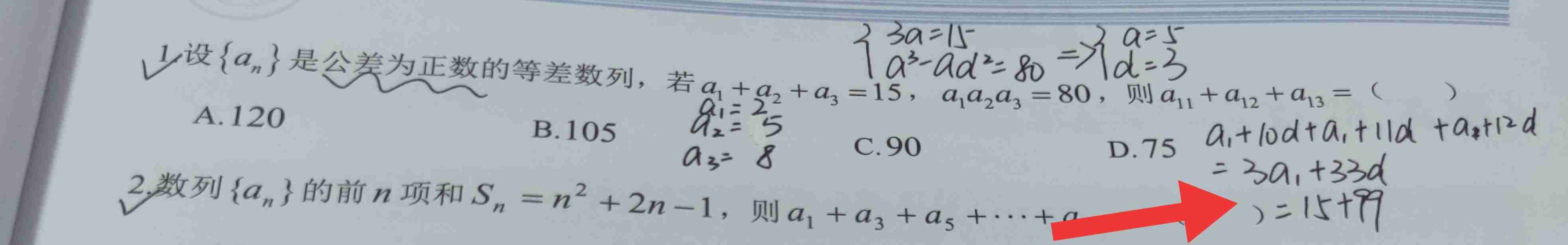曲谱自学网今天精心准备的是《高中数学数列解题技巧》，下面是详解！

可以把高中数学数列的几种解答方法归纳一下吗？譬...

请发到邮箱654307226@qq.com,谢谢Ps请用标准的数学符号，别用那种看起来极不舒服的...

请发到邮箱654307226@qq.com,谢谢
Ps 请用标准的数学符号，别用那种看起来极不舒服的

数列求和方法

1. 公式法：
等差数列求和公式:Sn=n(a1+an)/2=na1+n(n-1)d/2
等比数列求和公式：Sn=na1(q=1)
Sn=a1(1-qn)/(1-q)=(a1-an×q)/(1-q) (q≠1)
2.错位相减法
适用题型：适用于通项公式为等差的一次函数乘以等比的数列形式
{ an }、{ bn }分别是等差数列和等比数列. Sn=a1b1+a2b2+a3b3+...+anbn
例如：
an=a1+(n-1)d
bn=a1•q(n-1)
Cn=anbn
Tn=a1b1+a2b2+a3b3+a4b4....+anbn
qTn= a1b2+a2b3+a3b4+...+a(n-1)bn+anb(n+1)
Tn-qTn= a1b1+b2(a2-a1)+b3(a3-a2)+...bn[an-a(n-1)]-anb(n+1)
Tn(1-q)=a1b1-anb(n+1)+d(b2+b3+b4+...bn)
=a1b1-an•b1•qn+d•b2[1-q(n-1)]/(1-q)
Tn=上述式子/(1-q)

3.倒序相加法
这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个(a1+an)
Sn =a1+ a2+ a3+...... +an
Sn =an+ a(n-1)+a(n-3)...... +a1
上下相加 得到2Sn 即 Sn= （a1+an)n/2

4.分组法
有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.
例如：an=2n+n-1

5.裂项法
适用于分式形式的通项公式，把一项拆成两个或多个的差的形式，即an=f(n+1)－f(n)，然后累加时抵消中间的许多项。
常用公式：
（1）1/n(n+1)=1/n-1/(n+1)
（2）1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)]
（3）1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)]
（4）1/(√a+√b)=[1/(a-b)](√a-√b)
（5） n•n!=(n+1)!-n!
[例] 求数列an=1/n(n+1) 的前n项和.
解：an=1/n(n+1)=1/n-1/(n+1) （裂项）
则
Sn
=1-1/2+1/2-1/3+1/4…+1/n-1/(n+1)（裂项求和）
＝ 1-1/(n+1)
＝ n/(n+1)
小结：此类变形的特点是将原数列每一项拆为两项之后，其中中间的大部分项都互相抵消了。只剩下有限的几项。
注意： 余下的项具有如下的特点
1余下的项前后的位置前后是对称的。
2余下的项前后的正负性是相反的。

6.数学归纳法
一般地，证明一个与正整数n有关的命题，有如下步骤：
（1）证明当n取第一个值时命题成立；
（2）假设当n=k（k≥n的第一个值，k为自然数）时命题成立，证明当n=k+1时命题也成立。
例：
求证：
1×2×3×4 + 2×3×4×5 + 3×4×5×6 + …… + n(n+1)(n+2)(n+3) = [n(n+1)(n+2)(n+3)(n+4)]/5
证明：
当n=1时，有：
1×2×3×4 + 2×3×4×5 = 2×3×4×5×(1/5 +1) = 2×3×4×5×6/5
假设命题在n=k时成立，于是：
1×2×3×4 + 2×3×4×5 + 3×4×5×6 + …… + k(k+1)(k+2)(k+3) = [k(k+1)(k+2)(k+3)(k+4)]/5
则当n=k+1时有：
1×2×3×4 + 2×3×4×5 + 3×4×5×6 + …… + (k+1)(k+2)(k+3)(k+4)
= 1×2×3×4 + 2×3×4*5 + 3×4×5×6 + …… + k(k+1)(k+2)(k+3) + (k+1)(k+2)(k+3)(k+4)
= [k(k+1)(k+2)(k+3)(k+4)]/5 + (k+1)(k+2)(k+3)(k+4)
= (k+1)(k+2)(k+3)(k+4)*(k/5 +1)
= [(k+1)(k+2)(k+3)(k+4)(k+5)]/5
即n=k+1时原等式仍然成立，归纳得证

7.通项化归
先将通项公式进行化简，再进行求和。
如：求数列1，1+2，1+2+3，1+2+3+4,……的前n项和。此时先将an求出，再利用分组等方法求和。

8.并项求和：
例：1－2+3－4+5－6+……+（2n-1）-2n
方法一：（并项）
求出奇数项和偶数项的和，再相减。
方法二：
（1－2）+（3－4）+（5－6）+……+[（2n-1）-2n]

高中数学怎么复习会比较有效率

我今年高三，数学一直都不好，很差的那种，想在高考中取得较好成绩要如何复习呢？有没有比较有效率的方法...

我今年高三，数学一直都不好，很差的那种，想在高考中取得较好成绩要如何复习呢？有没有比较有效率的方法

一、 基础复习阶段──—系统整理，构建数学知识网络
第一轮复习，也称“知识篇”，在这一阶段，老师将带领同学们重温高一、高二所学课程，但这绝不只是以前所学知识的简单重复，而是站在更高的角度，对旧知识产生全新认识的重要过程。因为在高一、高二时，老师是以知识点为主线索，依次传授讲解的，由于后面的相关知识还没有学到，不能进行纵向联系，所以，你学的往往是零碎的、散乱的知识点，而在第一轮复习时，老师的主线索是知识的纵向联系与横向联系，以章节为单位，将那些零碎的、散乱的知识点串联起来，并将他们系统化、综合化，侧重点在于各个知识点之间的融会贯通。平时复习中应重视教材中概念、定理、公式等基础知识、基本技能；同时，更应注重知识的发展形成过程，例题的分析思路，求解过程。在复习中应立足教材、夯实基础，以课本为主，全面梳理知识、方法，注意知识结构的重组与概括。将高中阶段所学的数学知识进行系统整理，用简明的图表形式把基础知识进行有机的串联，构建成知识网络，使学生对整个高中数学体系有一个全面的认识和把握，以便于知识的存储,提取和应用，也有利于学生思维品质的培养和提高，这是数学复习的重要环节。第一轮重点是“三基”(基础知识、基本技能、基本方法)复习，目标是全面、扎实、系统、灵活。学生极易忽视复习课本重要例习题所蕴含的数学思想方法。如上海高考曾出现“解析几何重要思想方法为何”，江苏高考曾出现“用定义法求某函数的导数”等试题。《考试说明》明确指出：易、中、难题的占分比例控制在3：5：2左右，即中低档题占总分的80％左右，这就决定了我们在高考复习中必须抓基础，常抓不懈，只有基础打好了，做中低档题才会概念清楚，得心应手，做难题和综合题才能思路清晰，运算准确。所以大家在复习过程中应做到：
① 立足课本，迅速激活已学过的各个知识点。（建议大家在高三前的一个暑假里通读高一、高二教材）
② 注意所做题目使用知识点覆盖范围的变化，有意识地思考、研究这些知识点在课本中所处的地位和相互之间的联系。注意到老师选题的综合性在不断地加强。
③ 明了课本从前到后的知识结构，将整个知识体系框架化、网络化。
通观高中数学教材，是由一个大陆、一个半岛和一个群岛组成的。这个大陆，就是二维空间的形与数，涉及集合、映射与函数，方程与不等式，数列及其极限，直角坐标系下的点与数对、曲线与方程、曲线的交点、参数方程及相关参数的意义，导数及其应用；这个半岛，是指立体几何。它的体系与平面几何一脉相承，都是古典的公理体系，进行严密的推理论证，且立体几何问题一般都要化归为平面几何问题来加以解决。当然，还要特别关注向量这一工具的作用，总结出利用面向量解决立体几何问题的基本模式。这个群岛，是指离散数学撒在中学教材中的一些珍珠，如排列组合、二项式定理、概率与统计、数学归纳法等。中学数学内容的结构可看作是数与点的集合，数的集合形成了代数式、函数、复数集、排列与组合四大块，点的集合构成了图形，可分为平面图形(平面几何)、空间图形(立体几何)、坐标平面上的图形(解析几何)三大块，每块下面再列出具体的内容和要点，纵向横向联系，这就构成了中学数学知识网络图，如“函数”这部分纵横向联系的知识结构，能提炼解题所用知识点，并说出其出处。
④经常将使用最多的知识点总结起来，研究重点知识所在章节，并了解各章节在课本中的地位和作用。以下列举各章节的重点，供参考．
1．函数与不等式（主体）．代数以函数为主干，不等式与函数的结合是“热点’”．
（1）关于函数性质．单调性、奇偶性、周期性（常以三角函数为载体）、对称性及反函数等处处可考．常以具体函数，结合图象的几何直观展开，有时作适当抽象．这种题型较难，而通过找到一个符合条件的常见函数作为解决本题的入手是一个不错的方法.
（2）关于一元二次函数，是重中之重，有关性质及应用的训练要深入、广泛．函数值域（最值），以二次函数或转化为二次函数的值域，待别是含参变量的二次函数值域研究为重点；方法以突出配方、换元和基本不等式法为重点．一元二次方程根的分布与讨论，一元二次不等式解的讨论，二次曲线交点问题，都与一元二次函数，息息相关，在训练中应占较大比重．强化“三个二次式”的复习。
（3）关于不等式证明．与函数联系的不等式证明，与数列联系结合数学归纳法是重点．方法要突出比较法和利用基本不等式的公式法．对于放缩法虽不是高考重点，因历年考题中都或多或少用到放缩法，掌握几种简单的放缩技巧是必要的．证明不等式要善于分析式子结构特征和寻找已知求证之间的差异，从中找到与相关定理的联系来作为解决问题的突破口.
（4）关于解不等式．以熟练掌握一元二次不等式及可化为一元二次不等式的综合题型为目标，突出灵活转化，突出分类讨论．解不等式往往带有字母，需要讨论，还需要掌握转化、数形结合等方法以及函数与方程的思想和八种常见不等式的一般解法。
2．数列（主体）．以等差、等比两种基本数列为载体考查数列的通项、求和、极限等为重点．关于抽象数列（用递推关系给出的），不只限定“归纳一证明”，需加强．数列求和的几种方法，如并项、拆项，裂项、错位相减等常用方法必须掌握(注意对q的讨论)。
3．三角（非主体）．“调整意见”“对和差化积、积化和差的8个公式，不要求记忆”．考题难度不降．训练中要抓基本公式的熟练运用，突出正用、逆用和变式用. 三角问题主要有两种形式：一是求较为复杂的三角函数表达式的某些性质；二是三角形中有关边角的问题。凡是三角公式变换的问题都可以从分析角、函数类型和式子结构特征这三个方面的差异作为入手及解题的突破口。
4．复数（非主体，文科不考）．近几年呈降温趋势．训练题型、方法、难度等达到教材水准即可．
5．立体几何（主体）．
突出“空间”、“立体”．即把线线、线面、面面的位置关系考查置于某几何体的情景中．几何体以棱锥、棱柱为重点．棱柱中又以三棱柱、正方体为重点；棱锥以一条侧棱或一个侧面垂直于底面为重点，棱柱和棱锥的结合体也要重视．位置关系以判断或证明垂直为重点，突出三垂线定理及逆定理的灵活运用。
空间角以二面角为重点，强化三垂线定理定角法．空间距以点面距、线面距为重点，二者结合尤为重要．等积转化、等距转化是最常用方法．角、距离的计算最后都转化到一个三角形中进行。
面积、体积计算，解答题涉及棱锥（特别是三棱锥）居多．因为三棱锥体积求法灵活，思路广泛．
6．解析几何（主体）．
直线与圆锥曲线的方程、有关性质以及相互位置关系是重要内容。客观题照顾面，解答题应综合，直线与圆锥曲线的位置关系是高考主要题型，突出直线和圆锥曲线的交点、中点、弦长、轨迹是经常考查的问题，含参的范围问题是难点。突出与函数，向量的联系。
二、综合复习阶段──—综合深化，掌握数学思想方法
第二轮复习，通常称为“方法篇”。大约从第二学期开学到四月中旬结束。在这一阶段，老师将以方法、技巧为主线，主要研究数学思想方法。在复习中要注重把提高自己的数学能力作为目标，提高逻辑思维能力、运算能力、空间想象能力、分析问题和解决问题的能力、数学探究与创新能力。扩大新视野，完善高考要求的知识结构，优化思维品质，从根本上提高数学素养。这些都是数学复习中必须重点突破的方向与追寻的目标。学数学需要解题，但解题不是数学的全部，数学思想方法是数学的灵魂。不掌握数学思想方法的解题是蛮干，学数学而不解题则是“进了宝山空手而归”，不能掌握数学的真谛。老师的复习，不再重视知识结构的先后次序，而是以提高同学们解决问题、分析问题的能力为目的，提出、分析、解决问题的思路用“配方法、待定系数法、换元法、消元法，数形结合、分类讨论”等方法解决一类问题、一系列问题。第二轮复习一般是专题强化训练，目标在于提高学生解答高考解答题的能力。此阶段学生不应沉迷于套卷演练，而应在教师指导下，以典型例题为载体，以数学思想方法的灵活运用为线索，讲求解题策略，使自己在第一轮复习的基础上进行巩固、完善、综合、提高的重要阶段，要加强对思维品质和综合能力的培养，主要着眼于知识重组，建立完整的知识能力结构，包括学科的方法能力、思维能力、表达能力，但这都必须建立在知识的识记能力基础之上，理解知识的来源及其所蕴含的数学思想、数学方法，把握知识的纵横联系，培养探索研究问题的能力。第二轮复习要培养数学应用意识，学会从材料的情景、问题中去联系理论，能根据题目所给的材料，找到和主干知识的结合点。要学会形成体系和方法，即解题思路，包括对有效信息的提取、解题所需的方法和技巧、对事实材料的分析和判断及对结论的评价和反思等。不讲究方法的“刻苦”无异于蛮干。应该在理清基本概念、基本知识结构的基础上去做题，有时也可以在做题中加深对基础知识的理解。不注意总结解题规律和数学思想方法的解题是低效的，有时甚至是无意义的.同学们应做到：
①主动将有关知识进行必要的拆分、加工重组。找出某个知识点会在一系列题目中出现，某种方法可以解决一类问题。
②分析题目时，由原来的注重知识点，渐渐地向探寻解题的思路、方法转变。
③从现在开始，解题一定要非常规范，俗语说：“不怕难题不得分，就怕每题都扣分”，所以大家务必将解题过程写得层次分明，结构完整。
④适当选做各地模拟试卷和以往高考题，逐渐弄清高考考查的范围和重点。
三、强化复习阶段──—强化训练，提高应试实战能力
第三轮复习，大约一个月的时间，也称为“策略篇”。老师主要讲述“选择题的解法、填空题的解法、应用题的解法、探究性命题的解法、综合题的解法、创新性试题的解法”，教给同学们一些解题的特殊方法，特殊技巧，以提高同学们的解题速度和应试策略为目的。第三轮一般进行模拟、强化，目的在于调节学生智能、情感、意志等因素，使学生逐渐熟悉数学高考对学生的各项要求。此阶段学生应加强解题后反思，并舍得花一定的时间再次钻研考试大纲、考试说明及历届高考试题和各地的模拟试题，掌握高考信息、命题动向，提高正确率，练出速度，在练中升华到纯熟生巧的境界。在练习时要注意以下几点：解题要规范。俗话说，“不怕难题不得分，就怕每题都扣分”，所以务必将解题过程写得层次分明，结构完整。重要的是解题质量而非数量，要针对自己的问题有选择地精练。不满足于会做，更强调解题后的反思常悟，悟出解题策略、思想方法方面的精华，尤其是一些高考题、新题、难度稍大的题，这种反思更为重要，多思出悟性，常悟获精华。同学们应做到：
①解题时，会从多种方法中选择最省时、最省事的方法，力求多方位，多角度的思考问题，逐渐适应高考对“减缩思维”的要求。
②注意自己的解题速度，审题要慢，思维要全，下笔要准，答题要快。有时只是一个符号的误差，会让你体会到“失之毫厘，差之千里”的滋味，若在关键时候会让你抱憾终生。美国“哥伦比亚”号航天飞机返回地面时机毁人亡却源于一块绝缘瓦的故障。这些学习品质在以后工作中会让你受用终生。
③养成在解题过程中分析命题者的意图的习惯，思考命题者是怎样将考查的知识点有机的结合起来的，有那些思想方法被复合在其中，对命题者想要考我什么，我应该会什么，做到心知肚明。
四备考迎战阶段──心理调节，适应高考
最后，就是冲刺阶段，也称为“备考篇”。在这一阶段，老师会将复习的主动权交给你自己。以前学习的重点、难点、方法、思路都是以老师的意志为主线，但是，现在你要直接、主动的研读《考试说明》，研究近年来的高考试题，掌握高考信息、命题动向，并做到：
①检索自己的知识系统，紧抓薄弱点，并针对性地做专门的训练和突击措施（可请老师专门为你拎一拎）；锁定重中之重，掌握最重要的知识到炉火纯青的地步。
②抓思维易错点，注重典型题型。
③浏览自己以前做过的习题、试卷，回忆自己学习相关知识的历程，做好“再”纠错工作。
④博览群书，博闻强记，使自己见多识广，注意那些背景新、方法新，知识具有代表性的问题。
⑤不做难题、偏题、怪题，保持情绪稳定，充满信心，准备应考。考前指导主要包括四个方面的内容：常考易错的基础知识；常用的解题方法；考试解题的技巧；考试心理的指导。

求一些关于数列或三角函数的经典解题技巧(高中数学)

有没有详细点的讲解...

有没有详细点的讲解

高中数学题

为什么这样算不出结果？...

为什么这样算不出结果？

高中数学题不会做，先看答案显而易见是无效的，这会养成一个不好的习惯，导致考试是也离不开答案，但其实考试是没有答案的，因此，针对数学题不会做的情况，可能是思路没打通，或者基础没打好，就其中一点，我给一些我的浅见，希望对你有帮助。
1.很多学霸经验分享都说理科是完全靠理解，这个方法对于基础比较薄弱的同学真的不是那么适用，因为基础知识不牢固，代表可能连知识点都记不牢，既然基本都没掌握，谈何理解，因此，无论是背知识点还是例题，都要能够熟记到可以能够默写的程度；在背例题的时候要注意在背的同时，注意解题的思路；在背知识点，背例题可能没有立竿见影的效果，但是只要你能坚持下去，就一定能看见效果。
2.当你做题目的时候，你总会有一些思路，但是可能因为太过零碎，没有凑成完整地答题思路，这时候你选择去看答案，把答案抄下来，不要单纯地只会看答案抄答案，抄也要学会技巧。
3.建议每到周末都对自己的不会的题目做一下整理，如果不会的题目太多了，建议每3天总结一次，整理完题目之后记得要回顾，最好每天抽15分钟时间看看整理的题目。
4.通过整理题目，你会发现自己的漏洞，例如三角函数半角公式应用题，这个时候你就要开始找这样类型的专题进行强化。通过强化练习之后，以后遇到这样类型题就会得心应手。

澳门风云2粤语高清

植物大战僵尸动画版